大学入学共通テスト・目のつけどころ – 2025年 数学I・A 第1問
2025.04.15
受験への取り組み
2025年1月18日(土)・19日(日)に実施された「大学入学共通テスト」の「数学I,数学A」の問題を見ていきます。
いわゆる「解答・解説」みたいなものは、しっかりしたものが余所にたくさんあるので、ここではほぼやりません。
ここでは実際に解いてみて「ここは注意が必要だ」、「受験生にはこれを知っておいてもらいたい」というような気付きを簡単に紹介したいと思います。
きれいな問題用紙や解答・解説は、47NEWS(↓)や各新聞社・予備校などのHP、市販の過去問題集などをご覧ください。
https://www.47news.jp/culture/education/kyotsu-exam/2025
本来は大学入試センターのリンク(↓)を貼るべきですが、まだ最新年度の問題が更新されていない……
https://www.dnc.ac.jp/kyotsu/kakomondai/
とにかく時間が厳しい
今さら言うことでもないですが、とにかく共通テストは時間が厳しい試験です。
はっきり言って、共通テストの問題は個人的には好きではありません(というか大嫌いです)が、これで点数がついてしまうので、受験生はそんなことは言っていられません。
好まざると好まざるとにかかわらず、解くしかありません。
「数学I・A」の場合、第1問から第4問までの4問全問必答(つまり、選択問題なし)で、試験時間は70分。
今回、途中ちょっとつっかえてしまったところもあり20分かかってしまいましたが、これではいけません。
とにかく、問題を見た瞬間に「あれを使うんだ!」と気づく瞬発力と、「この問題はここまで」と見切る力が必要です。
そのためには、共通テストの形式に合わせた対策が必要不可欠です。
共通テストは特殊な試験です。
本番までの日数から逆算して、しっかり練習して対策して、本番に備えたいところです。
数学I・A 第1問
第1問は、「数学I」の「数と式」と「図形と計量」の分野から、配点30点の問題となっています。
〔1〕と〔2〕に分かれていて、〔1〕と〔2〕は独立しています。
〔1〕数と式
〔1〕は「数と式」の問題。

(1)の冒頭で「 a=1 とする。」とあって、「①の左辺は ② と表せる。」とあります。
ここで、
あ、①式に a=1 を代入すると、 x^2 の係数は 4b になって、あと同じようにするとたしかに②式になる。
で、②式を因数分解すると ア と イ が出る。
という思考の時間をいかに短縮できるか。
もはや何の試験なのかわかりませんが、とにかくプレッシャーのなか短時間で処理するのが、悪くも悪くも共通テストなのです。
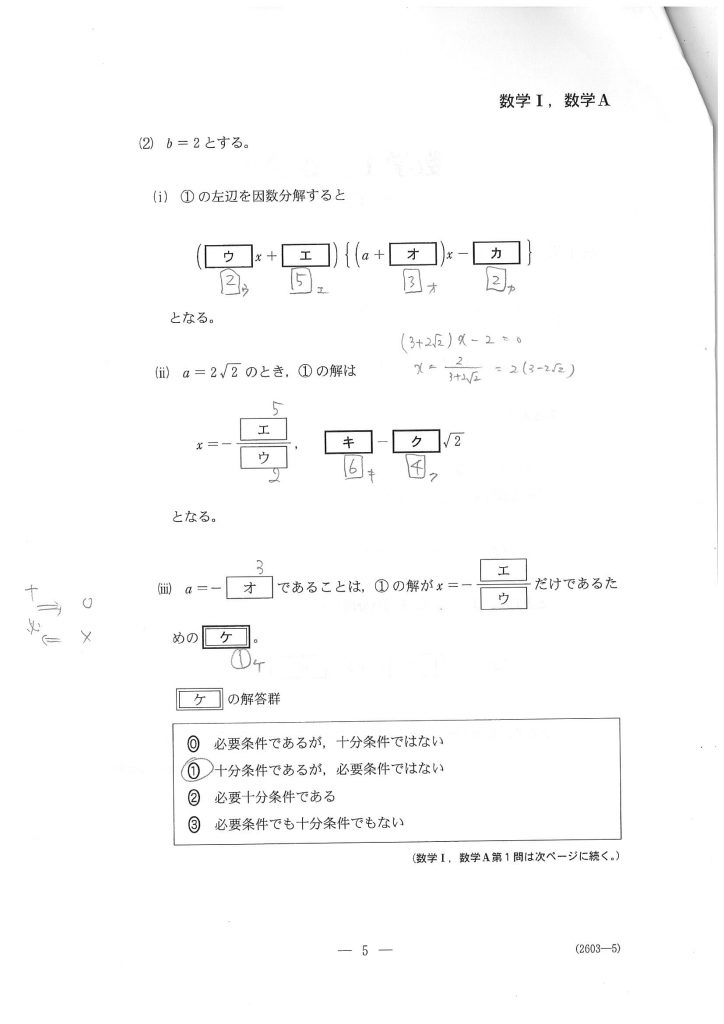
(2)は冒頭で「 b=2 とする。」とあります。
したがって、この「 b=2 」は(2)の最後まで生きる、こういうところにも意識を働かせてほしいです。
(i)と(ii)は時間をかければできる。その時間を短縮するのが難しいところです。
計算のテクニック的なものも身につけたいですね。
(iii)は、「⇒」と「⇐」に分けて考える。実はここでちょっと時間を使ってしまいました。
「⇒」は、a=-3 を代入すると、後ろのかっこは「 0・x -2 」になり、これがイコール0となるような x は存在しない。よって、前のかっこから出てくる -5/2 だけが解である。 → 真
「⇐」は、「①の解が -5/2 だけである」というのは、重解もあるではないか、と。
で、後ろのかっこの x に x=-5/2 を代入すると a=-19/5 となり(解いたときは計算しませんでしたが)、a=-3 だけとは限らない。 → 偽
よって、「十分条件であるが、必要条件ではない」の①が正解。
となりますが、時間がかかるようならパスでしょう。
(これは本番の話。勉強の際はじっくり時間をかけて考えてほしい問題です。いろいろな解きかたがあると思うので、解説サイトや過去問題集の解説を見比べてみるのもよいでしょう。)
〔2〕 図形と計量
続いて〔2〕は、打って変わって「図形と計量」の問題。
いったいこの問題文は何を言っているのか。
作問者および太郎さん花子さんにいかに素早く憑依できるか、数学以外の能力も問われます。
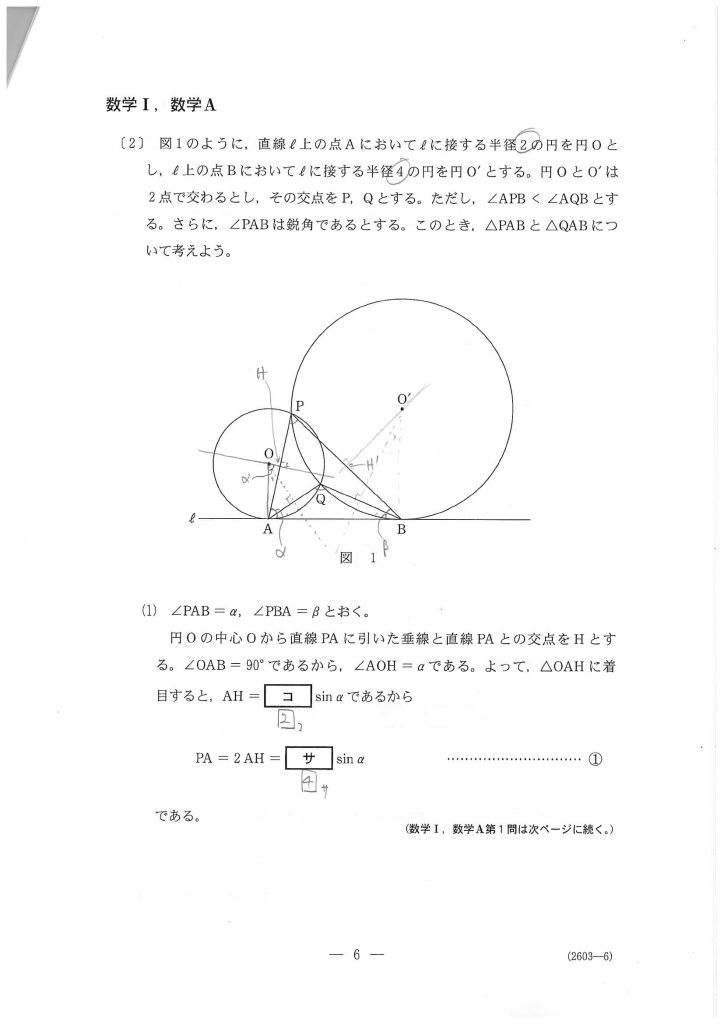
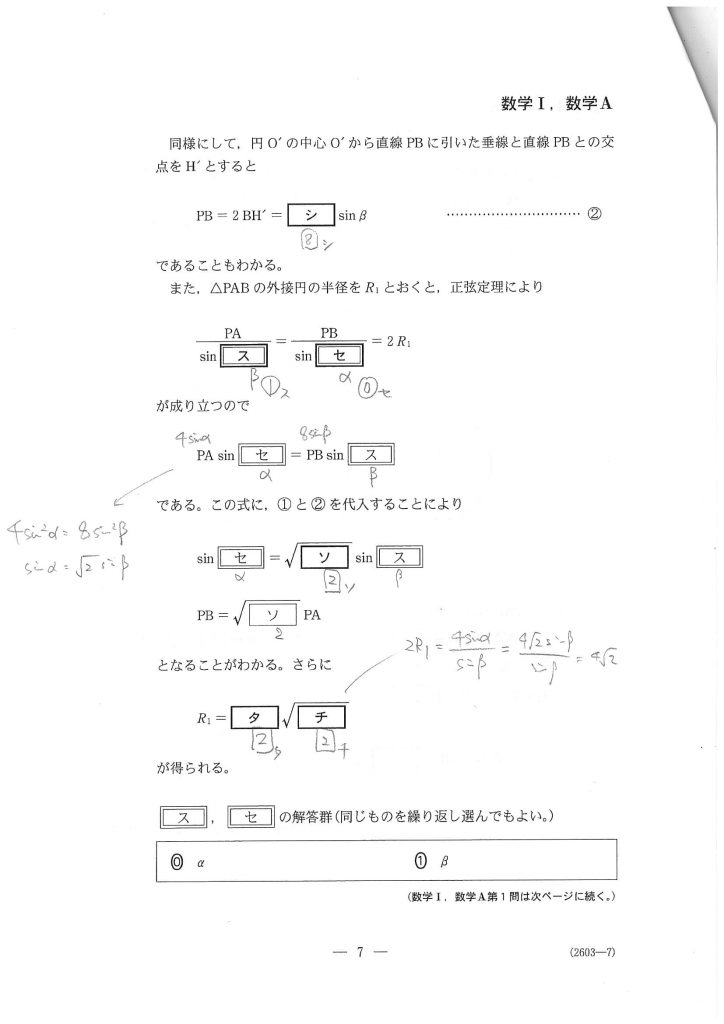
(1)は図にいろいろ書き込んで、いかに早く状況を把握できるか。
把握できれば図形の基本的な知識と正弦定理で最後までいけるのですが……
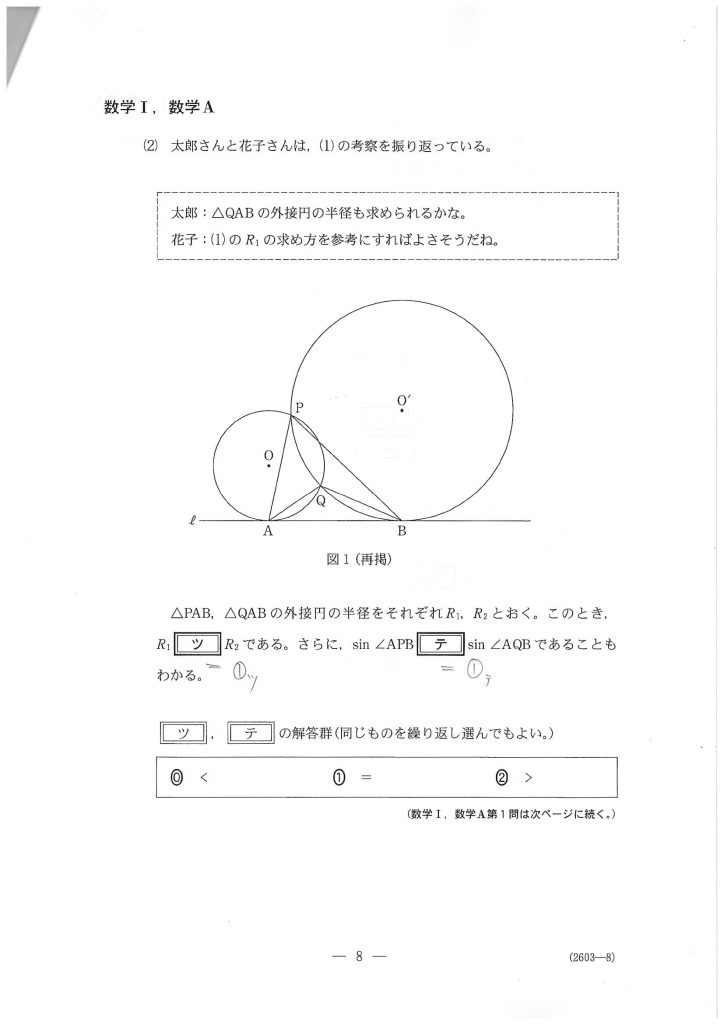
(2)は、「(1)と同様に考えると」のパターン。
共通テストで非常によく出てきます。
(1)で△PABについてぐだぐだごちゃごちゃやってきたことを、
△QABについてやるとどうなりますか?
という、個人的には大嫌いなパターンです。
一生懸命 コ サ シ ス セ ソ タ チ とやってきたことを、別の三角形でまた辿らされます。
頭のなかが整理されていないと焦ります。
時間がないなか、もはや受験生いじめと言っても過言ではない。
ともかく、「R1=R2」、結局同じであることにいかに早く気づけるか、という問題でした。

(3)は公式で解けるので、比較的平易かと。
ただ、ここに辿り着くまでに受験生は相当疲弊していると思います。
これでようやく、全4問中の第1問が終了。
70分の闘いはまだ始まったばかりです。
第2問につづく…… のか?
(リンク準備中)
●八戸市の下長、類家(青葉)にある人気の学習塾、勉強ナビの詳細は公式ホームページでご確認ください。こちらをクリック!!
●ライン@始めました。無料体験学習、資料請求、お問い合わせなどお気軽にラインからどうぞ!!

●ラジオ番組の内容はYouTubeからも確認できます。
チャンネルはこちらです。
関連記事
カテゴリー
- 塾長からのメッセージ (320)
- 勉強ナビの特徴 (42)
- 塾長が大切にしている事 (25)
- コース、授業内容、入会情報など (90)
- 各校舎の授業の様子など (535)
- 正しい勉強法 (54)
- 定期テストの取組み (12)
- 中学生 (12)
- 受験への取り組み (14)
- 大学入学共通テスト目のつけどころ (4)
- 青森県高校入試解答解説 (4)
- 中学受験 (1)
- 高校受験 (5)
- 大学受験 (1)
- 青森県高校入試情報 (57)
- 大学入試情報 (3)
- ラジオ番組放送内容 (302)
人気の記事
-
1

「チーム勉強ナビ U-12」放課後の時間を変える小学生向け新コース
塾長からのメッセージ
-
2

★ 2026年2月の入会特典 ★
塾長からのメッセージ
-
3

【共通テスト】第2日程平均点中間発表 難易度はどうだったのか? 来年以降に向けても
塾長からのメッセージ
-
4
成績票の見かた / 素点、平均点、学年順位、偏差値
類家青葉校
-
5
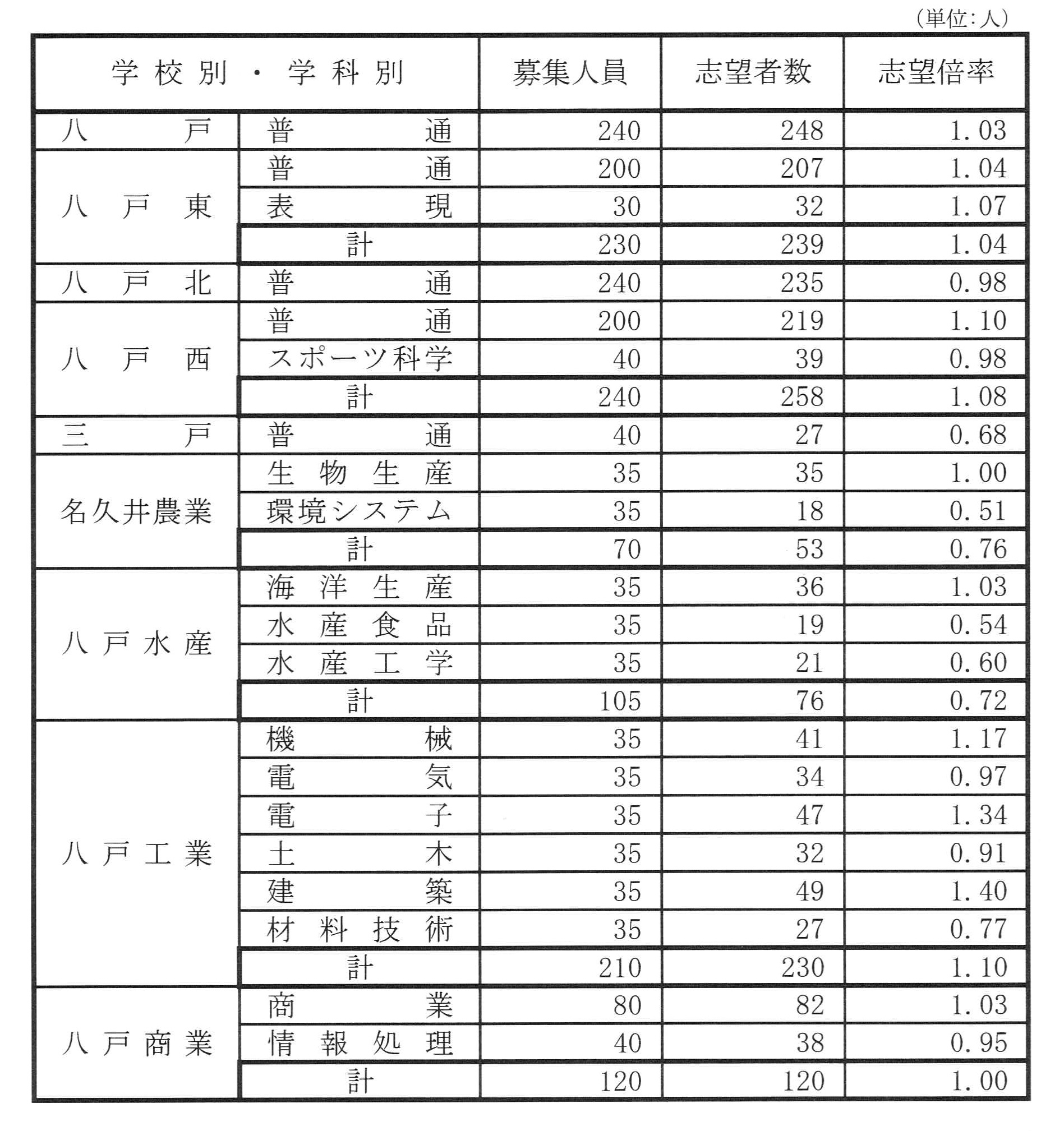
令和3年度青森県立高校入試志望倍率(第2次調査)-青森県教育委員会発表
塾長からのメッセージ
-
6

令和2年度定期テストの勉強法②/学校のワークの効率の良い勉強について
塾長からのメッセージ
-
7

中学生の自主勉強ノートの作成方法について
ラジオ番組放送内容
月別アーカイブ









