青森県立高校入試 解答と解説 – 令和7年度 数学 大問1
2025.04.15
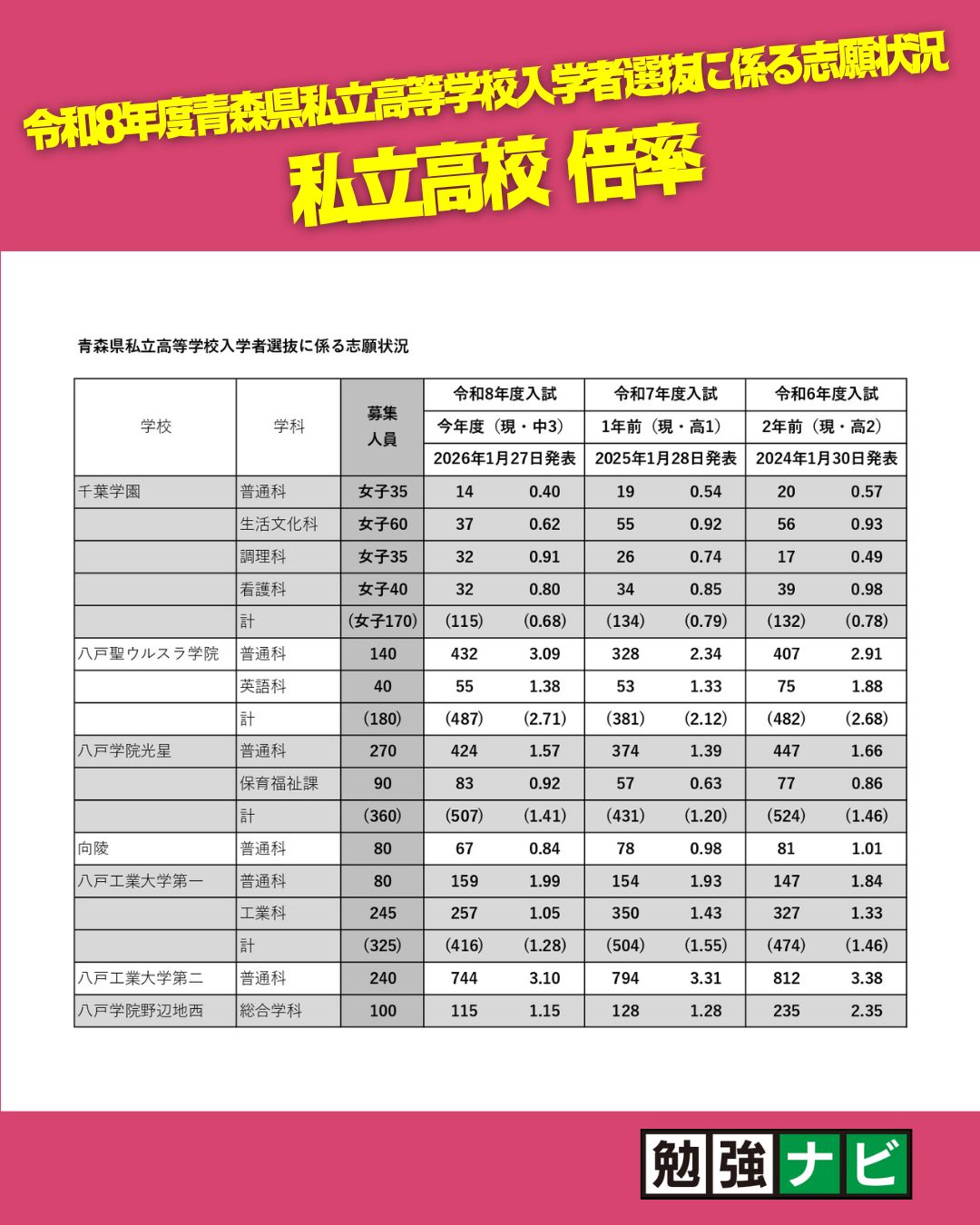
受験への取り組み
2025年3月5日(水)に実施された「令和7年度 県立高等学校入学者選抜学力検査」数学の大問1、解答・解説です。
文字だけではなかなか解説しづらいところもありますが、とりあえず行ってみましょう。
問題は下のリンク(青森県教育委員会HP)または市販の過去問集などをご覧ください。
https://www.pref.aomori.lg.jp/soshiki/kyoiku/e-gakyo/sembatsu25_nyuusenmondai.html
大問1 講評
数学・大問1はいわゆる「小問集合」で、配点は43点。非常に大きいです。
この43点というのは過去30年以上続いている、青森県立高校入試の不変の伝統であるとも言えます。
(なぜか平成18年度(2006年度)だけ44点でしたが、例外はその年ぐらいです。)
1問ごとの配点が大きいのも特徴です。
(1)ア~オの5問が1つ3点で15点、(2)~(8)の7問が1つ4点で28点、合計43点。
基本問題が多く、周りの受験生もみんな得点してくるので、解ける問題の取りこぼしは許されません。
いかにミスせず、短時間で処理できるかが、高得点をとるための鍵となります。
今年のセットでは、極端な難問や不意打ち問題はなかったように思います。
八・北・東の受験生なら、43点満点を目指したいところです。
まずは前半(問題用紙2ページ)です。
↓ 画像が表示されない場合は再読み込みしてください。

(1)ア 【中1 正の数・負の数】 3点
これは絶対に間違えてはいけません。
-11+4=-7
これで3点です。
(1)イ 【中1 正の数・負の数】 3点
これも落とせない問題。
( )を計算して、{ }を計算して、最後に5とかけ算します。
これも3点。
(1)ウ 【中2 式の計算】 3点
これも超基本問題。
マイナスの後ろの( )の符号を間違えないように。
3点。
(1)エ 【中2 式の計算】 3点
わり算が2つ並んでいるのが、県立高校入試としてはちょっと珍しいパターンです。
やりかたはいくつかありますが、わり算を逆数のかけ算に変えるとミスしにくいと思います。
符号は、「+わる-わる+だから、-」とはじめに決めてしまう(または最後に確認する)とミスしません。
3点。
(1)オ 【中3 平方根】 3点
分母にルートがあったら、分母の有理化です。
ルート8とかルート18とか、大きな数のルートを見たらまずは数を出せないか考えましょう。
これも基本問題、確実にとりたいところです。
3点。
ここまで1つ3点、計15点です。
(2)【中1 文字の式(不等式)】4点
「おとな9人にa枚ずつ、子ども8人にb枚ずつ配る」 → 9a+8b
「余った」ということは、9a+8b(枚)が、150(枚)より少なかったということ。
よって、9a+8b<150 が正解です。
150(枚)から 9a+8b(枚)を配った残りが0枚より多いと考えて、150-(9a+8b)>0 などでもOKです。
ここから1つ4点です。
(3)【中1 データの活用(相対度数)】 4点
この問題、できなかった人は必ず教科書で「相対度数」を調べてください。
(啓林館2021年度版なら、1年生の225ページです。)
相対度数 = 階級の度数 / 度数の合計
( / は分数を表します。「階級の度数」が分子、「度数の合計」が分母。)
度数の合計は、さくらんぼ全部の個数で、 3+11+12+4=30(個)
階級の度数は、7 g以上 9 g 未満の階級の個数で、12(個)
よって、求める相対度数は、 12/30 = 0.4
なお、模範解答は 0.40 で、「0.4 でも正解とする」と書いてあります。
(というか、本問は模範解答を0.4として、「0.40でも正解とする」が正しい気もするが…… )
4点。
(4)【中3 二次方程式】 4点
「解の公式」一発の問題です。
この問題の正答率はかなり高いと思われます。
絶対にミスしないように。
4点。
続いて、後半(問題用紙3ページ)です。
↓ 画像が表示されない場合は再読み込みしてください。

(5)【中2 場合の数と確率】 4点
上の画像のとおり、樹形図をかきましょう。
すると、AとBのくじのひきかたは全部で20とおりで、そのうち2人とも当たりくじをひくのは ①-② と ②-① の2とおり。
したがって、求める確率は、 2/20 = 1/10 となります。
4点。
(6)【中2 図形の調べ方・図形の性質と証明】 4点
△DBCで、∠D=90°、∠C=44°だから、
∠B=180°-(90°+44°)=46°
また、△DBC≡△EBA (証明は省略)より、
BC=BA となるので、△BCAは二等辺三角形
底角は等しいので、∠BAC=∠BCA= x+44°
△BCAで、46°+(x+44°) ×2=180°
これを解いて、x=23°
△ABC ≡ △EBD なので、∠ABC = ∠EBD です。
∠ABC と ∠EBD の両方に ∠ABD が含まれているので引くと、∠DBC = ∠EBA で、∠EBA = 20° です。
斜線をつけた三角形で、△DEB = 180° -(125°+20°) = 35°
△ABC ≡ △EBD なので、∠x = ∠CAB = ∠DEB = 35° です。
合同な三角形に気づけるか、また、大きな三角形(△ABC)が二等辺三角形であることに気づけるか、がポイント。
4点。
(7)【中1 データの活用】 4点
「適切でないもの」を選ぶ問題です。気をつけましょう。
ア 10回続けて投げると、表が3回出る場合がある。 → そりゃあ、あるでしょう。
イ 20回続けて投げると、表と裏が10回ずつ出る。 → とは限らないでしょう。
ウ 2000回続けて投げると、表と裏がおよそ1000回ずつ出ると予想できる。 → まあ、そうなるでしょう。
エ 投げる回数が多いほど、表の出る相対度数のばらつきは小さくなり、その値は0.5に近づく。 → まあ、そうなるでしょう。
……と、ちょっと解説になっていませんが、まあ明らかに イ ということでよいでしょう。
とにかく「適切でないもの」の部分を見落とさないこと、これに尽きる問題です。
(8)【中1 変化と対応(比例)】 4点
比例の基本問題。
まず、グラフが直線で原点を通る → 比例 → 「 y = ax 」とおける、という流れ。
そして、x=30 のとき y=24 で、y=18 のとき x がいくらであればよいか、ということが読み取れるか。
あとは上の画像に書いた計算で答えを出します。
x=22.5(45/2) となるので、「22分30秒後」で答えます。
これがたとえば x=22.8 だったり、x=67/3 だったりしたら、きちんと「22分48秒後」、「22分20秒後」と答えられるか、中学生の皆さんは確認しておきたいところです。
(リンク準備中)
●八戸市の下長、類家(青葉)にある人気の学習塾、勉強ナビの詳細は公式ホームページでご確認ください。こちらをクリック!!
●ライン@始めました。無料体験学習、資料請求、お問い合わせなどお気軽にラインからどうぞ!!

●ラジオ番組の内容はYouTubeからも確認できます。
チャンネルはこちらです。
関連記事
カテゴリー
- 塾長からのメッセージ (316)
- 勉強ナビの特徴 (42)
- 塾長が大切にしている事 (23)
- コース、授業内容、入会情報など (88)
- 各校舎の授業の様子など (530)
- 正しい勉強法 (52)
- 定期テストの取組み (12)
- 中学生 (12)
- 受験への取り組み (14)
- 大学入学共通テスト目のつけどころ (4)
- 青森県高校入試解答解説 (4)
- 中学受験 (1)
- 高校受験 (5)
- 大学受験 (1)
- 青森県高校入試情報 (55)
- 大学入試情報 (3)
- ラジオ番組放送内容 (297)
人気の記事
-
1

★ 2026年2月の入会特典 ★
塾長からのメッセージ
-
2

★ 2月の考査に向けて、勉強ナビでは「超テスト対策」を実施します(中1・中2) ★
定期テストの取組み
-
3

【共通テスト】第2日程平均点中間発表 難易度はどうだったのか? 来年以降に向けても
塾長からのメッセージ
-
4
成績票の見かた / 素点、平均点、学年順位、偏差値
類家青葉校
-
5
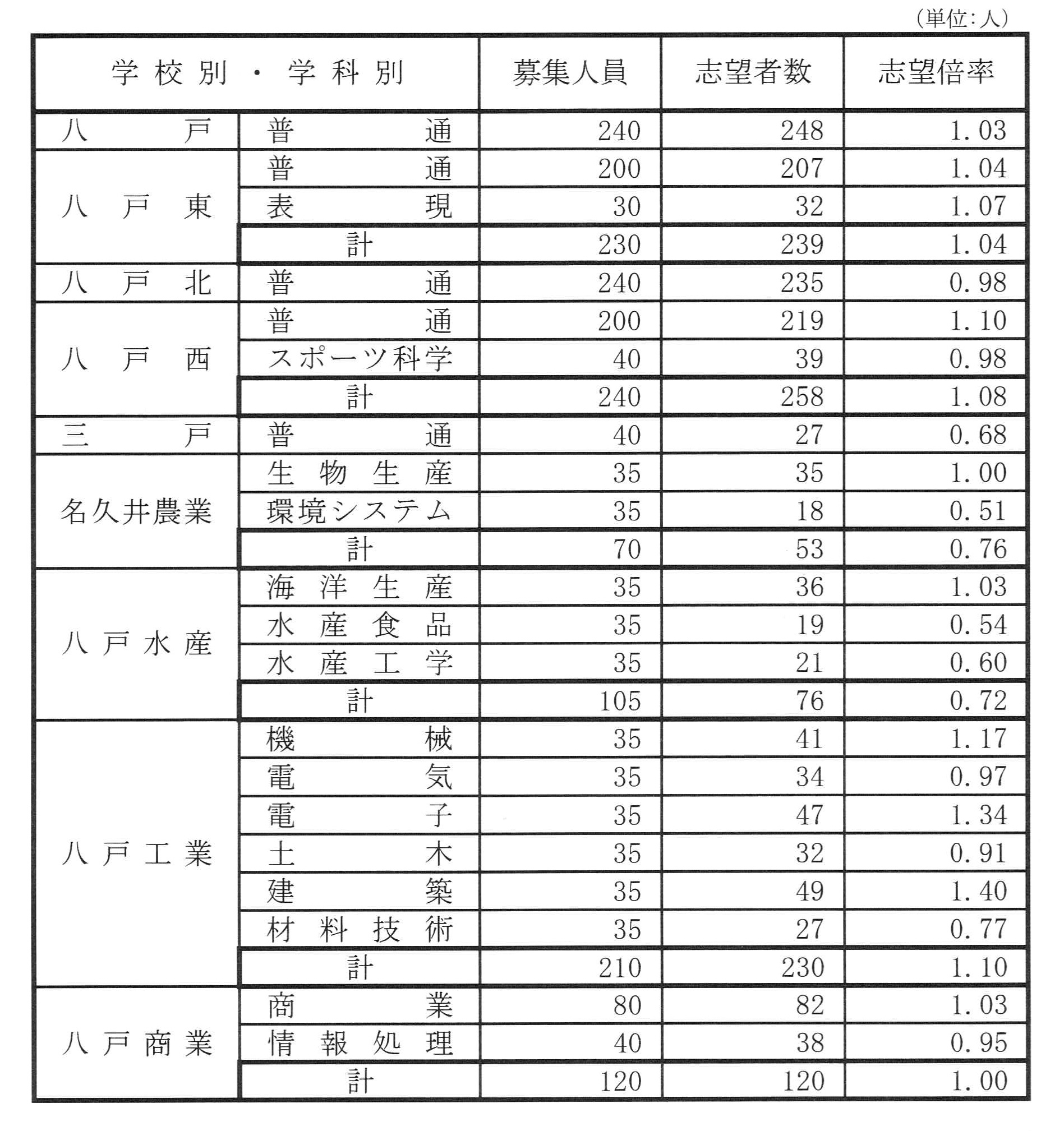
令和3年度青森県立高校入試志望倍率(第2次調査)-青森県教育委員会発表
塾長からのメッセージ
-
6

令和2年度定期テストの勉強法②/学校のワークの効率の良い勉強について
塾長からのメッセージ
-
7

中学生の自主勉強ノートの作成方法について
ラジオ番組放送内容
月別アーカイブ