算数・数学の学年別復習ポイント（小5・小6・中1・中2／冬休みにやっておきたいこと）

中3は入試まであと75日

明日12月23日（金）は市内小中学校の終業式。
明後日12月24日（土）から冬休み。勉強ナビの冬期講習も始まります。

中3生は志望校も確定し、いよいよ入試までのロングスパートに入ります。
定期考査も終わり、ここからは範囲を限定しない本当の入試対策に集中できる時期になります。
中学3年間の学習内容から苦手箇所を集中的に克服しつつ、全範囲から出題される入試問題に対応できる応用力や、時間配分や見なおし箇所、場合によっては問題を「捨てる」判断などの含め、一人ひとりの目標に合わせた作戦も考えていきます。

小5・小6・中1・中2 学年別復習ポイント

今日のテーマは「小5・小6・中1・中2 学年別復習ポイント」です。
二学期の学習内容はどの学年も分量が多く、苦手箇所になりやすく次の学年の学習にも影響が大きい単元が含まれています。
学校の授業が進まず、まとまった時間を勉強に充てられる冬休みを利用して、しっかり復習して三学期を迎えたいところです。

小5

小5の二学期は、「整数」「分数」「面積」「平均とその利用」「単位量あたりの大きさ」「割合」などを習いました。

何といっても、「単位量あたりの大きさ」と「割合」が難しいところです。
ちょうど今の時期は「割合」を勉強していますが、問題文を読んで状況をいかに理解するかがポイントになります。
● 割合＝比べる量÷もとにする量
● 比べる量＝もとにする量×割合
● もとにする量＝くらべる量÷割合
いわゆる「く・も・わ」は、できれば使いたくないと考えていますが、まずは問題を解けるようにならないとおもしろくないので、導入として使わざるを得ない場合が多いです。

また、問題文のなかで、どれが「もとにする量」で、どれが「比べる量」なのかがわからないお子さんもいます。
ちょっと大変ですが、できるだけ簡単な例で、ある程度の量をこなして身につけなければなりません。

解けるようになって、割合のイメージがついてきたら、「く・も・わ」からの卒業を目指したいところです。
まとまった時間をつくれる冬休みが、そのチャンスです。

そのほかの単元の項目を列挙すると、以下のとおりです。
「整数」 …… 偶数・奇数、倍数と公倍数、約数と公約数
「分数」 …… 等しい分数、分数のたし算・引き算、わり算と分数、分数と小数・整数の関係
「面積」 …… 三角形の面積、平行四辺形の面積、台形・ひし形の面積、面積の求め方のくふう、面積と比例
「平均とその利用」 …… 平均、平均を使って

いずれも、小6以降の算数・数学の土台になるものばかりです。
すべての単元について、しっかりマスターしておきたいところです。

小6

小6の二学期は、「円の面積」「立体の体積」「比とその利用」「図形の拡大と縮小」「およその形と大きさ」「比例と反比例」「表を使って考えよう」などを習いました。

最大の難所は、やはり「比例と反比例」でしょう。
中学数学につながる重要単元です。
比例か反比例か、あるいはどちらにもならないかの判定、一方の値がわかっているとき他方の値を求める計算、グラフのかきかたなど、ポイントがたくさんあります。
さらに、図形の面積や周の長さ、道のり・速さ・時間など、小5算数の復習も必要になり、お子さんひとりで学校の宿題や問題集を解き進めるのは難しい内容です。
可能であれば、塾か保護者の方がしっかりついてみてあげたいところです。

「円の面積」も、つまずきやすい単元です。
● 円の面積＝半径×半径×円周率（小6）
● 円周＝直径×円周率（小5）
結局は、この公式を覚えて使いこなせなければなりません。

円を小さいおうぎ形に切り刻んで並べ替えて長方形をつくってその面積を求めるという公式の導出過程は、教科書にも書いてあり理想としては理解してほしいところですが、ほとんどの小学生には難しすぎるようです。
公式丸暗記は気が進みませんが、この単元に関しては「はんけいかけるはんけいかけるさんてんいちよん」と繰り返し唱えて覚えるしかないと思います。

そのほかも、すべての単元が重要ですが、「表を使って考えよう」は、表をかかないと問題も解けないし理解も定着しません。
面倒がらずに冬休みの宿題やワークで復習しておきたいところです。

中1

中1の二学期で学習した内容です（学校により多少の進度差があります）。
「第3章 方程式」
「第4章 変化と対応」

この冬でどこに力を入れるかは、数学が得意かそうでないかで変わってきます。

数学が得意なら、応用問題を集中的に

二学期までの範囲でどんな問題が出てもだいたいできるという中1生は、「★印」がついていたり「C問題」だったり、持っている問題集のなかでも難しい問題だけを拾って解いてみるとよいでしょう。
足りなければ、塾の教材や市販の問題集を追加しましょう。

二学期までの範囲で解けない問題がある中1生は、まずはその解きなおしです。
解きなおすべき問題に印をつけて、冬休み中に2周ぐらいできれば、かなりの実力がつくと思います。
計算問題は宿題で出されると思いますので、特に不安がなければ、応用問題を集中的にやってほしいところです。

数学が苦手なら、まずは計算問題を

冬休み明け三学期の内容は、「平面図形」「空間図形」「資料の活用」です。
そのいずれも、結構な計算力が要求されます。

おうぎ形の面積、弧の長さ、立体の体積や表面積、平均値、相対度数など、考えかたも大事ですが、その過程で四則演算（たし算・ひき算・かけ算・わり算）を大量にミスなく行わなければなりません。
計算に苦労して時間がかかりすぎるようであれば、内容の理解どころではなくなってしまいます。

教科書でも学校や塾の教材でもなんでもかまいません。
第1章「正負の数」から、章末問題にある計算問題だけを拾って解いてみましょう。
解けるようなら次の章へ。解けなかったらその場で復習です。
計算以外の問題は、今は飛ばしましょう。
まずは計算のしかたを覚えてミスなく答えを出せるようになることで自信がつきますし、次のテストでの点数も間違いなく上がります。

中2

中2の二学期で学習した内容です（学校により多少の進度差があります）。
「第2章 連立方程式」の文章題
「第3章 一次関数」
「第4章 図形の調べ方」
「第5章 図形の性質と証明」

いずれも、入試頻出の重要な単元です。
中2は、3段階に分けてみます。

数学が得意なら、「一次関数の利用」と「図形の証明問題」

数学が得意だ、数学で点数を稼ぎたい、という中2生は、高校入試を意識して一次関数の応用問題を解いてほしいと思います。
高校入試では例年、[4] に関数の問題、さらに [5] で総合的な数学力を問う問題が出題されています。
今年度の中3生を見ていてもそうですが、この分野を教科書レベルから入試レベルに引き上げるのには時間がかかります。
また、[5] は近年は長い問題文や図表から状況を読み取り、必要な条件を整理して、筋道を立てて解く難問になっています。
その過程で関数の知識や考え方が必要になります。

塾に通っていればその都度適切な課題を追加しますし、学校で渡されたワークや市販の問題集でもよいと思います。
いろいろな種類の問題に触れて、この根本にある考え方をこの冬で習得してほしいです。

余裕があれば「図形の証明問題」か「連立方程式の利用」のどちらか苦手なほうを頑張ってみましょう。

数学がやや苦手なら、「一次関数の基本」

数学が平均点ぐらいかすこし下ぐらいなら、一次関数の基本をしっかりマスターしてほしいところです。
入試や実力テストでいえば、（1）や（2）の問題。
傾き・変化の割合、グラフの交点、x 軸や y 軸との交点などを求める問題は、中2のうちに完璧にしましょう。
解きかたは決まっていますが、機械的に覚えるのではなく、意味を理解したうえで答えを導き出せるようにしたいです。
ただ、そのためにはある程度の数をこなさなければならないと思います。
これをマスターできているかどうかで、中3実力テストの成績が変わってきます。

余裕があれば図形の証明問題や連立方程式の文章題もやりたいところです。
ですが、まずは「一次関数の基本」をやってみて、時間が足りないようであれば、これ一本に絞ったほうが効果的で充実した冬休みになると思います。

数学が苦手なら、まずは「計算問題」

二学期は、一次関数や証明問題など、計算力、理解力、記述力が求められる難しい単元が続きました。
学校の授業を聞いていても、正直なところまったくわからないという中2生もいると思います。
その場合は、二学期の内容はひとまず置いて、中1と中2・一学期の復習をしましょう。

中1と同様に、教科書でも学校や塾の教材でもなんでもかまいません。
中1の第1章から、章末問題にある計算問題だけを拾って解いてみましょう。
解けるようなら次の章へ。解けなかったらその場で復習です。
計算以外の問題は、今は飛ばしましょう。
まずは計算のしかたを覚えてミスなく答えを出せるようになることで自信がつきますし、次のテストでの点数も間違いなく上がります。

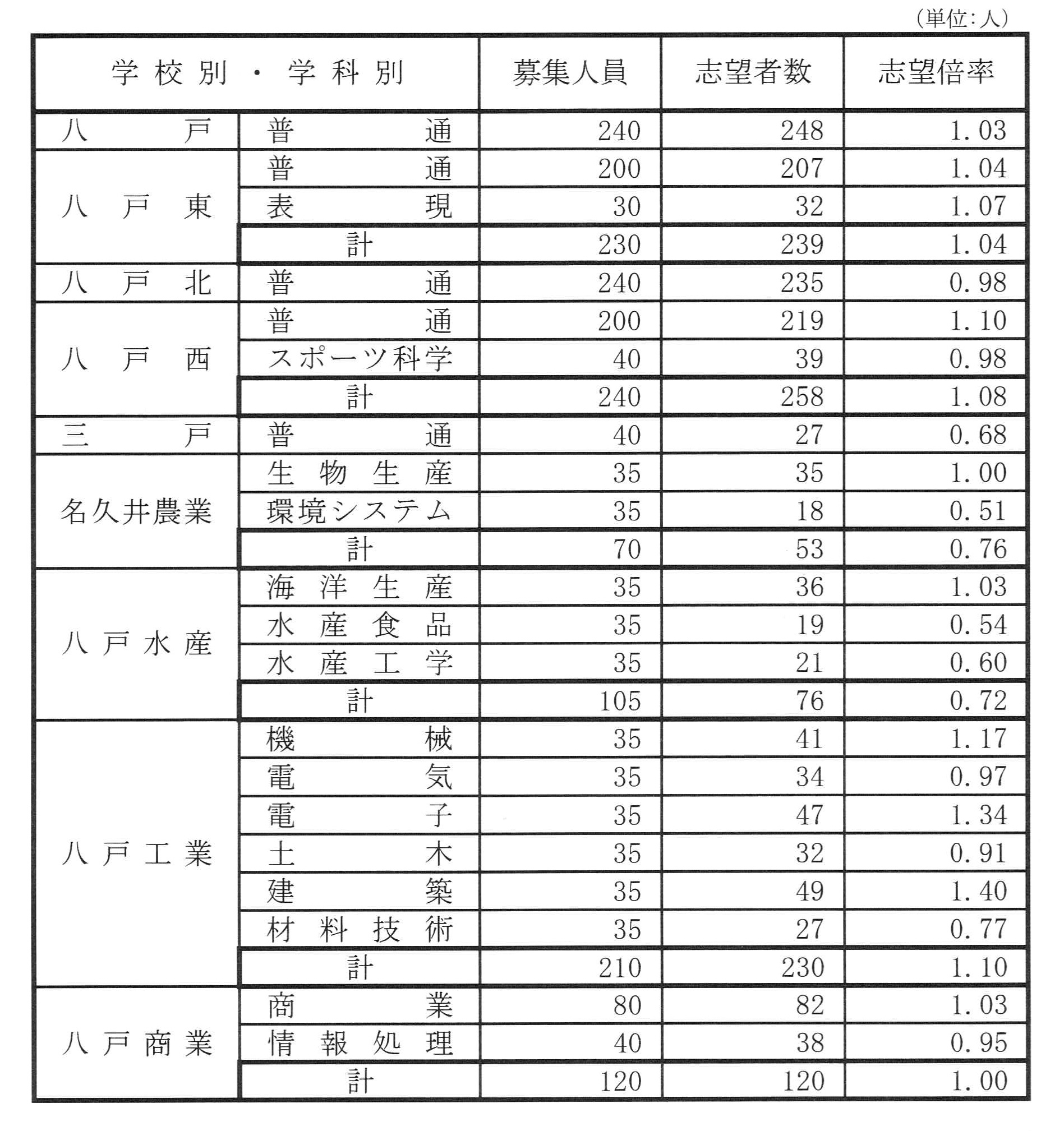
令和5年度青森県立高校入試志望倍率（第1次調査）－青森県教育委員会発表

２０２３年１月３１日までの入会特典

県立高校入試まで あと75日
私立高校入試まで あと49日