大学入学共通テスト・目のつけどころ – 2025年 数学I・A 第4問
2025.04.30
受験への取り組み
2025年1月18日(土)・19日(日)に実施された「大学入学共通テスト」の「数学I,数学A」の問題を見ていきます。
いわゆる「解答・解説」みたいなものは、しっかりしたものが余所にたくさんあるので、ここではほぼやりません。
ここでは実際に解いてみて「ここは注意が必要だ」、「受験生にはこれを知っておいてもらいたい」というような気付きを簡単に紹介したいと思います。
きれいな問題用紙や解答・解説は、47NEWS(↓)や各新聞社・予備校などのHP、市販の過去問題集などをご覧ください。
https://www.47news.jp/culture/education/kyotsu-exam/2025
本来は大学入試センターのリンク(↓)を貼るべきですが、まだ最新年度の問題が更新されていない……
https://www.dnc.ac.jp/kyotsu/kakomondai/
とにかく時間が厳しい
今さら言うことでもないですが、とにかく共通テストは時間が厳しい試験です。
はっきり言って、共通テストの問題は個人的には好きではありません(というか大嫌いです)が、これで点数がついてしまうので、受験生はそんなことは言っていられません。
「数学I・A」の場合、第1問から第4問までの4問全問必答(つまり、選択問題なし)で、試験時間は70分。
とにかく、問題を見た瞬間に「あれを使うんだ!」と気づく瞬発力と、「この問題はここまで」と見切る力が必要です。
そのためには、共通テストの形式に合わせた対策が必要不可欠です。
共通テストは特殊な試験です。
本番までの日数から逆算して、しっかり練習して対策して、本番に備えたいところです。
数学I・A 第4問
第4問は、「数学A」の「場合の数と確率」の分野から、配点20点の問題です。
他の第1問~第3問に比べてかなり平易で分量も少なく、解きやすい問題ではなかったでしょうか。
得意な受験生なら10分かからずに、うまくいけば5~6分ぐらいで処理できるかも。
とはいえ、共通テスト特有の数学長文読解問題ですから、問題の設定を把握するのには結構頭を使います。
第1問から順番に解く受験生であれば、第4問に到達する頃にはかなり疲弊しているはずです。
集中力を切らさずに解くには、勉強のスタミナも必要です。
また、この「場合の数と確率」は、人によって得意不得意が大きく分かれる分野です。
前述のとおり、得意な人はさらさらっと10分かからずに20点とってしまえる問題です。
苦手な人は第4問にどう対峙するか、戦略面での準備もしておきたいところです。

(1)
(1)は平易です。
問題文を正確に読み取ること、これに尽きます。
なお、(1)の結果は(2)、(3)でも使います。
ここを間違えると大変なことになるので、落ち着いてミスのないよう処理しましょう。
(2)
(2)は期待値の問題。
これも「易」に分類されるでしょう。
セ の問題は、誰にとって妥当であるかを間違わないこと。
問題文では、「主催者が負担する金額X円の期待値が、参加料の金額500円未満であるとき、主催者は参加料の設定は妥当であると判断し、(以下略)」とあるので、これに従えば、期待値450円は「妥当である」となります。
セ が含まれる文も、主語は「主催者は」であり、主催者にとって妥当か否かが問われています。
参加者にとって妥当か否かではありません。
ところで、今から30年ぐらい前のセンター試験なら、この(2)ぐらいまでの問題で50点とれたんですよね。
……というのは、今の高校生の前では口が裂けても言えない内緒の話。

(3)
(3)の(i)は、計算のテクニック(というほどでもないですが)を使うと、時間を短縮できます。
170×(3/16)+340×(1/8)+510×(11/16)
という計算をするわけですが、170、340、510は当然170の倍数なので、170でくくってしまいます。
また、確率・期待値の問題は分母をそろえます。
すなわち、まわりが 3/16、11/16 で分母が16なので、1/8 も 2/16 と考える。
すると、全体を 170/16 でくくることができて、計算が一気に楽になります。
……というようなことは、特に指導しなくても自然に思いつく高校生も多いです。
しかし一方で、おもむろに「170×(3/16)」と「340×(1/8)」と「510×(11/16)」を別々に計算してそれらを足し合わせる、という非効率極まりない計算をする高校生もまあまあいます。
1月までにいろいろな手法を身につけて、時間の短縮と正確性の確保をしていきたいですね。
(ii)の前半は、(2)の(ii)と同じで、問題文に従って判断する問題。
後半は、(i)で a=170 としてやってきたことを、一般の a に戻してもう一度考えてみよう、という問題。
共通テスト特有の “同じ道たどらせ” 問題です。
ちょっと頭が振られますが、落ち着いて処理しましょう。
以上で「数学I・A」終了です。
次回、「数学II・B・C」につづくのでしょうか?
(リンク準備中)
●八戸市の下長、類家(青葉)にある人気の学習塾、勉強ナビの詳細は公式ホームページでご確認ください。こちらをクリック!!
●ライン@始めました。無料体験学習、資料請求、お問い合わせなどお気軽にラインからどうぞ!!

●ラジオ番組の内容はYouTubeからも確認できます。
チャンネルはこちらです。
関連記事
カテゴリー
- 塾長からのメッセージ (319)
- 勉強ナビの特徴 (42)
- 塾長が大切にしている事 (24)
- コース、授業内容、入会情報など (90)
- 各校舎の授業の様子など (533)
- 正しい勉強法 (52)
- 定期テストの取組み (12)
- 中学生 (12)
- 受験への取り組み (14)
- 大学入学共通テスト目のつけどころ (4)
- 青森県高校入試解答解説 (4)
- 中学受験 (1)
- 高校受験 (5)
- 大学受験 (1)
- 青森県高校入試情報 (57)
- 大学入試情報 (3)
- ラジオ番組放送内容 (301)
人気の記事
-
1

「チーム勉強ナビ U-12」放課後の時間を変える小学生向け新コース
塾長からのメッセージ
-
2

★ 2026年2月の入会特典 ★
塾長からのメッセージ
-
3

★ 2月の考査に向けて、勉強ナビでは「超テスト対策」を実施します(中1・中2) ★
定期テストの取組み
-
4

【共通テスト】第2日程平均点中間発表 難易度はどうだったのか? 来年以降に向けても
塾長からのメッセージ
-
5
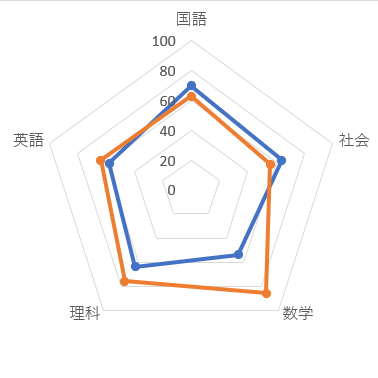
成績票の見かた / 素点、平均点、学年順位、偏差値
類家青葉校
-
6
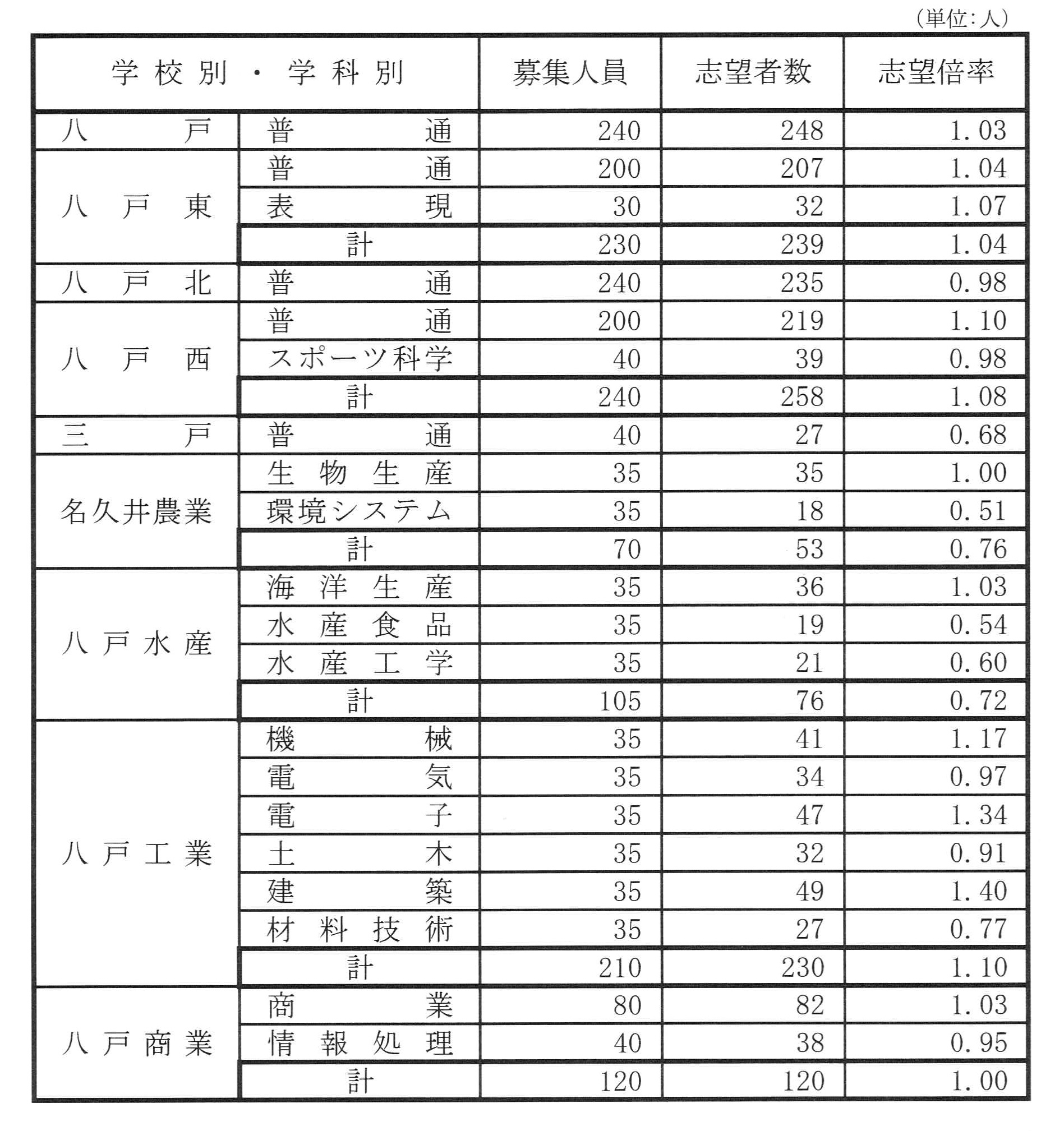
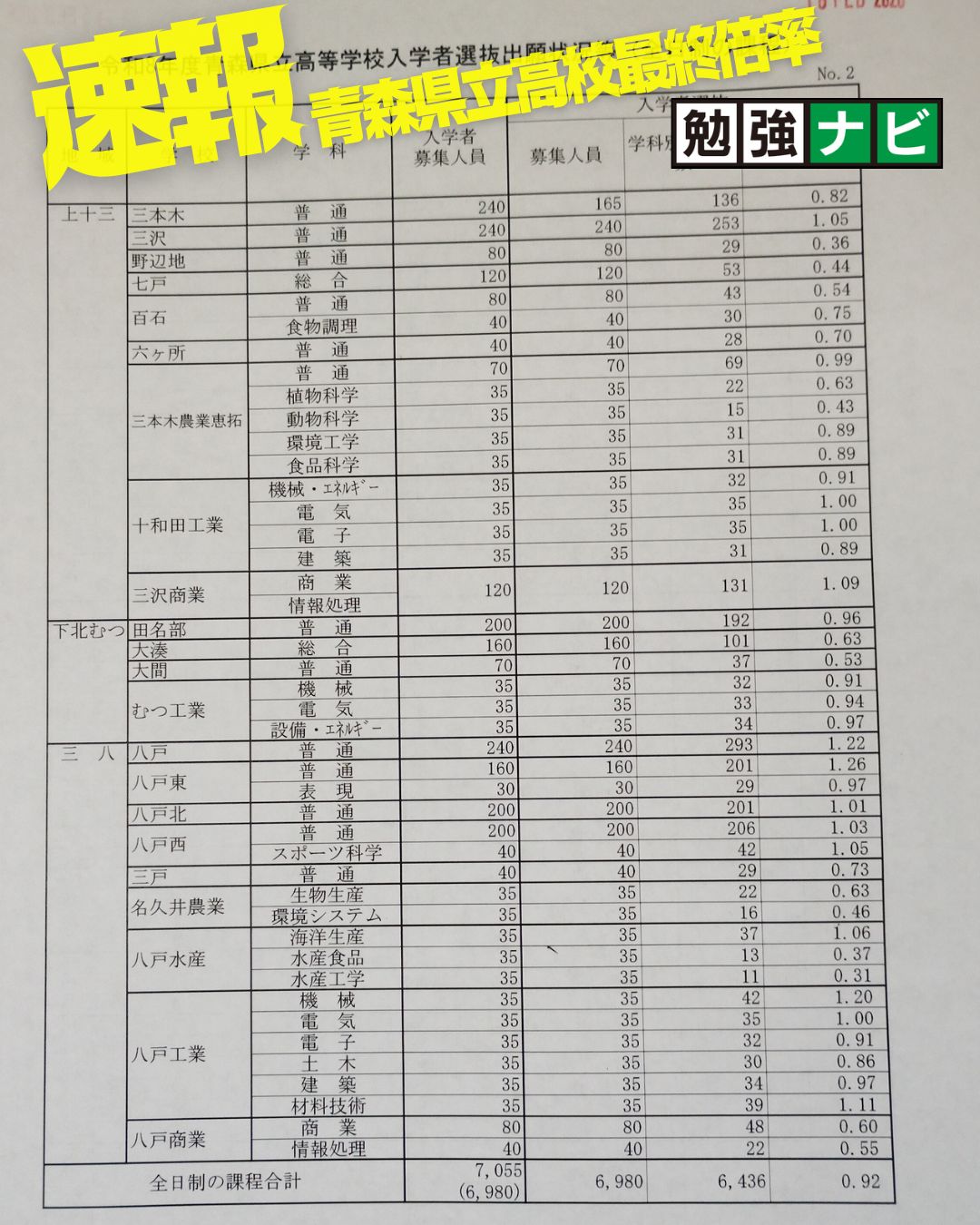
令和3年度青森県立高校入試志望倍率(第2次調査)-青森県教育委員会発表
塾長からのメッセージ
-
7

令和2年度定期テストの勉強法②/学校のワークの効率の良い勉強について
塾長からのメッセージ
-
8

中学生の自主勉強ノートの作成方法について
ラジオ番組放送内容
月別アーカイブ