青森県立高校入試 解答と解説 – 令和7年度 数学 大問2
2025.04.18
受験への取り組み
2025年3月5日(水)に実施された「令和7年度 県立高等学校入学者選抜学力検査」数学の大問2、解答・解説です。
文字だけではなかなか解説しづらいところもありますが、とりあえず行ってみましょう。
問題は下のリンク(青森県教育委員会HP)または市販の過去問集などをご覧ください。
https://www.pref.aomori.lg.jp/soshiki/kyoiku/e-gakyo/sembatsu25_nyuusenmondai.html
大問2 講評
数学の大問2は12点で、(1)と(2)の独立した2つの小問に分かれています。
一方は比較的「軽量級」の単発問題。
もう一方は謎の人物「レンさん」と「メイさん」の会話を題材とした問題です。
大学入学共通テストの「太郎さん」と「花子さん」を彷彿とさせます。
ところで、なぜ「レンさん」と「メイさん」なのでしょうか。
いろいろ調べてみたのですが、結局よくわかりません。
ということで、「謎の人物」としています。
近年、大問2はだいたい以下の分野から出題されています。
※ 平成28年度=2016年度以降。
※ 複数の分野にまたがっている問題や分類が難しい問題もありますので、あくまで参考ということでご覧ください。
※ また、ここに挙げた分野は大問1や大問5で出題されることもあります。
| 出題分野 | 出題年度 |
| 作図 | 令7 令5 令4 平31 |
| 文字式の利用 | 令7 令3 令2 |
| 資料の整理 | 令6 平31 平29 |
| 連立方程式 | 令6 平30 平29 |
| 確率 | 令5 令4 令3 令2 平30 |
| 整数の性質 | 令4 |
| 標本調査 | 平28 |
| 二次方程式 | 平28 |

(1)【中1】作図 3点
(1)は作図の問題。
青森県立高校入試では毎年、「作図」(令7 令5 令4 平31 平27)か、「グラフの描画」(令3 令2 平30 平29 平28)のどちらかが出題されています。
(近年で唯一の例外は令和6年度ですが、この年は大問5で記述問題(短いですが)が出ているので、これがその代わりでしょうか?)
「作図」が出題されるときは、この大問2に配されます。
今回は、「直線 ℓ 上に、2点A、Bを通る円の中心Oを作図によって求めなさい。」という問題。
「中心Oから2点A、Bまでの距離は円の半径で等しくなる」 → 「線分ABの垂直二等分線だ!」 の流れですが、これはどんな問題集にも載っている頻出問題なので、しっかりクリアしたいところです。
【注意!】
線分ABの垂直二等分線と直線 ℓ との交点をグリグリっとやって、「O」と書き込むのを忘れないでください。
「中心 O を作図によって求めなさい」という問題なので、「O」を書かないと不正解もしくは大減点です。
なお、教育委員会発表の模範解答は弧をつなげていませんが、つなげてもつなげていなくても、どちらでも大丈夫です。
(2)【中3】レンさんメイさん問題/式の計算の利用 9点
謎の人物「レンさん」と「メイさん」が登場する(2)です。
問題自体は、これもいろんな問題集でよく見かけるパターンと言えるでしょう。
P は(右上)×(左下)、Q は(左上)×(右下)ですね。
そして、4すみのうち一番小さい「左上」を n とすると、「右上」はそれより1大きい n+1 、「左下」は 左上より14大きい n+14 、「右下」はそれより1大きい n+15 となります。
あとは、画像にあるように計算して、結果は 14 になります。
正解は、
あ n+1(2点)
い n+14(2点)
う n+15(2点)
え n^2+15n(エヌの2乗プラス15エヌ)(3点)
八・北・東志望者は確実に12点とりたいところ。
それ以外の高校を志望する人も、比較的易しい問題なので12点を目指したいところです。
ところで、(2)の あ と い と う は all or nothing(全部できるか全部できないか)の可能性が高いので、ここに配点6点というのはちょっと大きすぎるのでは?
(リンク準備中)
●八戸市の下長、類家(青葉)にある人気の学習塾、勉強ナビの詳細は公式ホームページでご確認ください。こちらをクリック!!
●ライン@始めました。無料体験学習、資料請求、お問い合わせなどお気軽にラインからどうぞ!!

●ラジオ番組の内容はYouTubeからも確認できます。
チャンネルはこちらです。
関連記事
カテゴリー
- 塾長からのメッセージ (316)
- 勉強ナビの特徴 (42)
- 塾長が大切にしている事 (23)
- コース、授業内容、入会情報など (88)
- 各校舎の授業の様子など (530)
- 正しい勉強法 (52)
- 定期テストの取組み (12)
- 中学生 (12)
- 受験への取り組み (14)
- 大学入学共通テスト目のつけどころ (4)
- 青森県高校入試解答解説 (4)
- 中学受験 (1)
- 高校受験 (5)
- 大学受験 (1)
- 青森県高校入試情報 (55)
- 大学入試情報 (3)
- ラジオ番組放送内容 (297)
人気の記事
-
1

★ 2026年2月の入会特典 ★
塾長からのメッセージ
-
2

★ 2月の考査に向けて、勉強ナビでは「超テスト対策」を実施します(中1・中2) ★
定期テストの取組み
-
3

【共通テスト】第2日程平均点中間発表 難易度はどうだったのか? 来年以降に向けても
塾長からのメッセージ
-
4
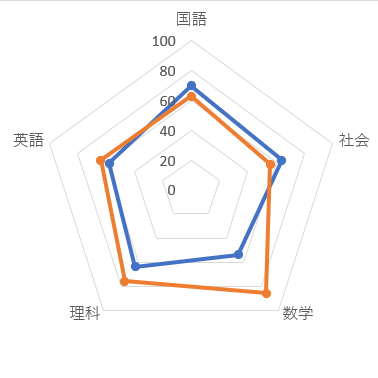
成績票の見かた / 素点、平均点、学年順位、偏差値
類家青葉校
-
5
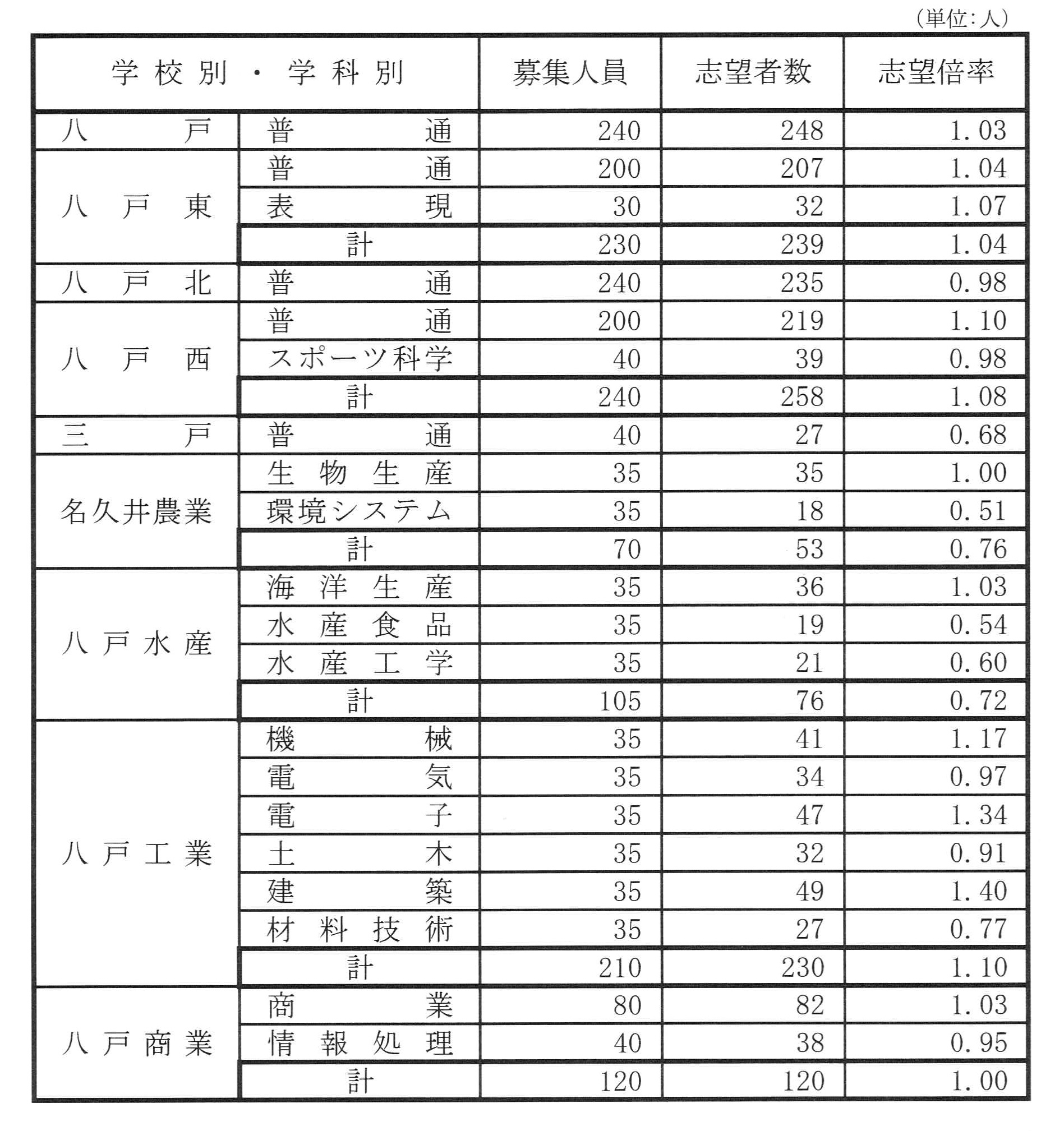
令和3年度青森県立高校入試志望倍率(第2次調査)-青森県教育委員会発表
塾長からのメッセージ
-
6

令和2年度定期テストの勉強法②/学校のワークの効率の良い勉強について
塾長からのメッセージ
-
7

中学生の自主勉強ノートの作成方法について
ラジオ番組放送内容
月別アーカイブ